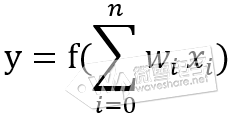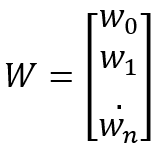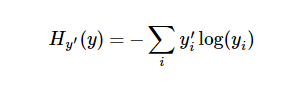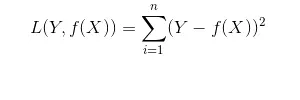Jetson Nano系列教程7：TensorFlow入门介绍(二)
一、前言
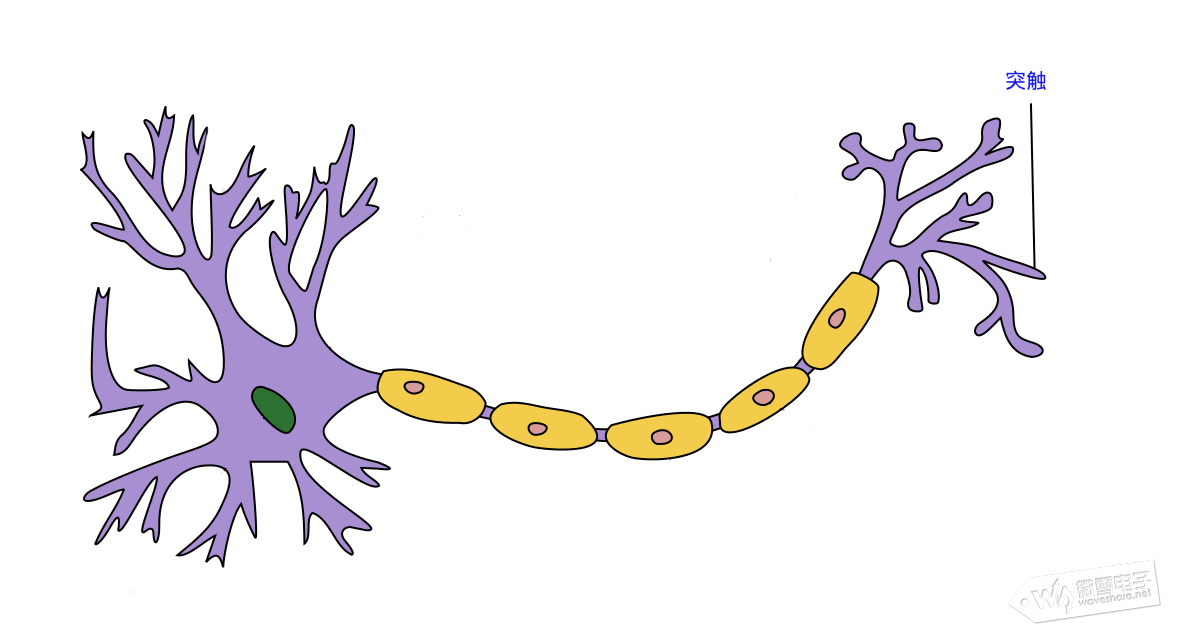
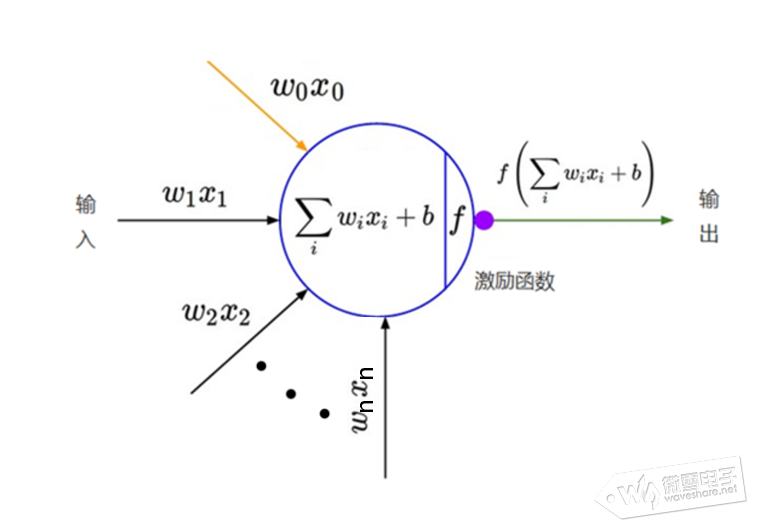
这一篇分享神经网络(NN)的激励函数，损失函数等相关内容，并用TensorFlow构建运行一个神经网络。 二、神经网络(NN)的激励函数，损失函数、梯度下降法 ①、激励函数 什么是激励函数？与上一篇提到神经网络逼近或拟合任意连续函数能力之间有什么关系？ 从神经元数学描述出发，神经元之间传递的信息，可理解权重值W为信息传递到下一神经元的强度，b表示神经元的阈值或偏置，对来自上一层所有输入信息产生输出信息的变换关系就是激励函数，如下图
图中y表示神经元输出，函数f称为激活函数 ( Activation Function )或转移函数 ( Transfer Function ) 若将阈值b看成是神经元的一个输入x0的权重W0，则上面的式子能够简化为：
设输入向量X=[x0,x1,x2,...,xn],权重和偏值为向量W
则神经元的数学模型为y=f(XW)，对于一个二层神经网络(输入层不算一层)，假设输入层神经元的输出为：
O1 = F1( XW1 )
则第一层(也称隐藏层)的输出为：
O2 = F2 ( F1( XW1 ) W2 )
则输出层(第二层)的输出为：
O3 = F3( F2 ( F1( XW1 ) W2 ) W3 )
若激活函数F1~F3都选用线性函数，那么神经网络的输出O3将是输入X的线性函数。因此，若要做高次函数的逼近就应该选用适当的非线性函数作为激活函数。对于对于多达上百层的的深度网络(DNN)也可证明若使用线性函数作为激活函数时，输入输出只是线性变换。
这里分享相关文章讲解为什么神经网络有逼近任意连续函数能力以及证明:
举个例子，信号与系统分析中的傅里叶变换章节，解释了用无穷个不同频率的弦波信号生成方波信号类似逼近过程的原理，
感兴趣读者可点击参阅相关内容
。
常用非线性的激活函数有sigmoid，ReLu，tansh，softsign，ELU等。
（1)、sigmoid函数常用在浅层神经网络，将输入变换到(0,1)区间
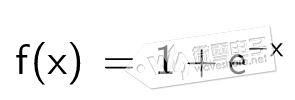
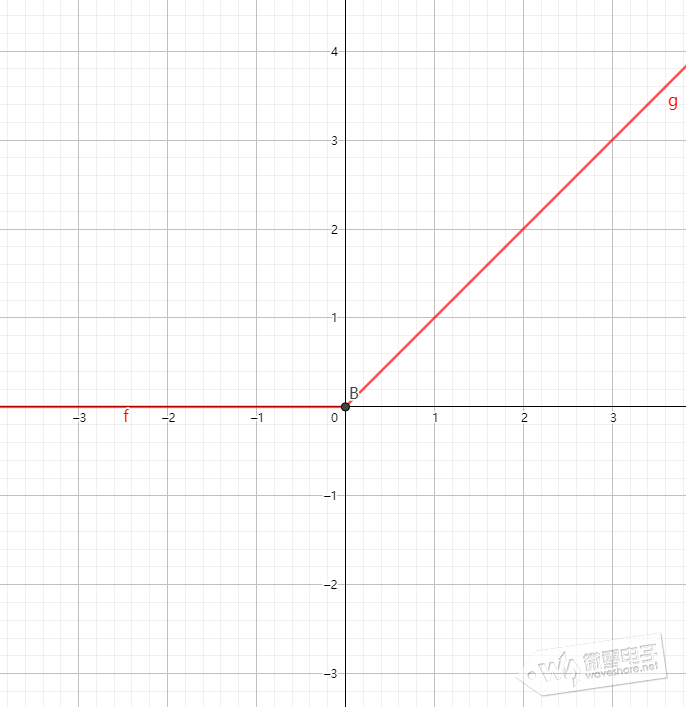
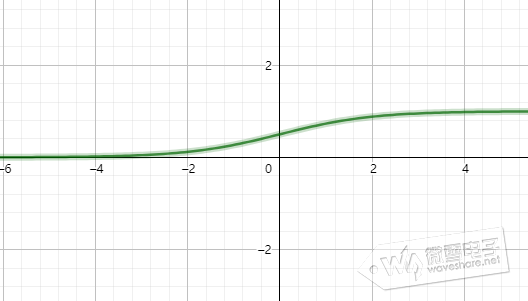（2）、ReLu线性整流函数，将输入变换到Max(0,x)区间
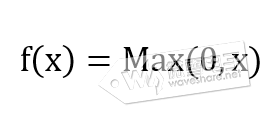
(3)、tanh双曲正切函数，将输入变换到(-1,1)区间
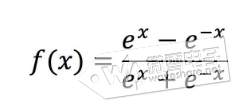
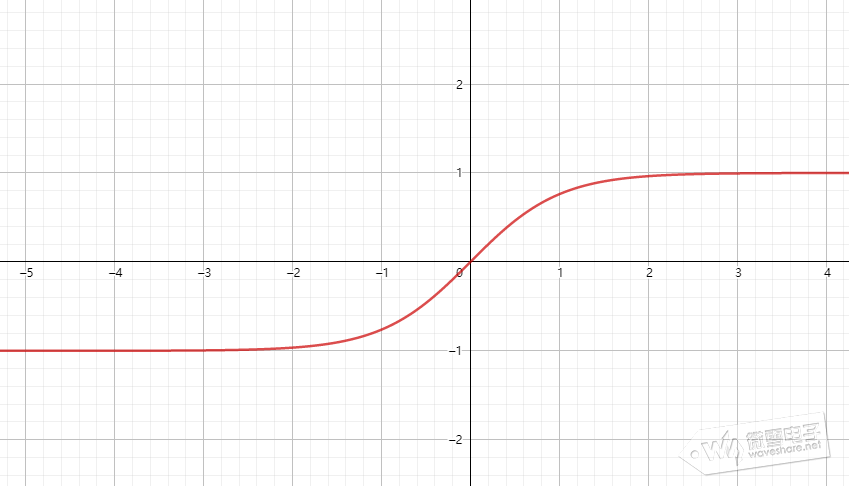了解更多激活函数请点击我参考。
tensorflow使用激活函数的用法是：
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers,Sequential
tf.keras.layers.Dense(512,activation=tf.nn.relu)#构建一层由512个神经元，激活函数为relu神经网络
tf.keras.layers.Dense(256,activation=tf.nn.sigmoid)#构建一层由256个神经元，激活函数为sigmoid神经网络
tf.keras.layers.Dense(128,activation=tf.nn.tanh)#构建一层由128个神经元，激活函数为tanh神经网络
②、损失函数 什么是损失函数？
在机器学习中通常定义指标来表示一个模型是坏的，这个指标称为成本（cost）或损失（loss），然后尽量最小化这个指标。通俗理解是预测结果和样本目标结果相差多少，比如，输入一张牧羊犬样本图片到一个神经网络，若第一次训练后输出一张鱼的预测图片，接下来每次训练输出预测结果分别是鸡、羊等越来越靠近犬这个物种，说明这个神经网络模型权重偏置等参数在往犬这个物种靠近，损失函数逐渐减小。 常用的损失函数有交叉熵(cross-entropy)、平方损失函数、均方误差函数等。 交叉熵常用在分类问题上，产生于信息论里面的信息压缩编码技术，但是它后来演变成为从博弈论到机器学习等其他领域里的重要技术手段，如0-9手写数字分类问题中输出10个值为概率分布，其中最大值表示对应数字(0-9共10个数字)的可能性最大。它的定义如下:
y 是我们预测结果（训练结果）, y' 是样本目标结果。比较粗糙的理解是，在多输出神经网络上，交叉熵是用来衡量我们的预测用于描述真相的低效性。
平方损失函数是线性回归问题常用损失函数，一般用在具体数值的预测，例如一年四季某城市用电量预测，房价预测等。
损失函数详细分析请参考下面相关文章
tensorflow中用到的损失函数有tf.nn.relu, tf.nn.elu, tf.nn.softmax, tf.nn.softsign等。 对于分类问题，可以这样定义损失函数，其中softmax_cross_entropy_with_logits函数将训练结果转化成概率分布。
#y_为样本目标结果，y为样本训练结果
loss = tf.nn.softmax_cross_entropy_with_logits(y, y_)
对于回归问题，可以这样定义损失函数
loss = tf.reduce_mean(tf.square(y_ - y))
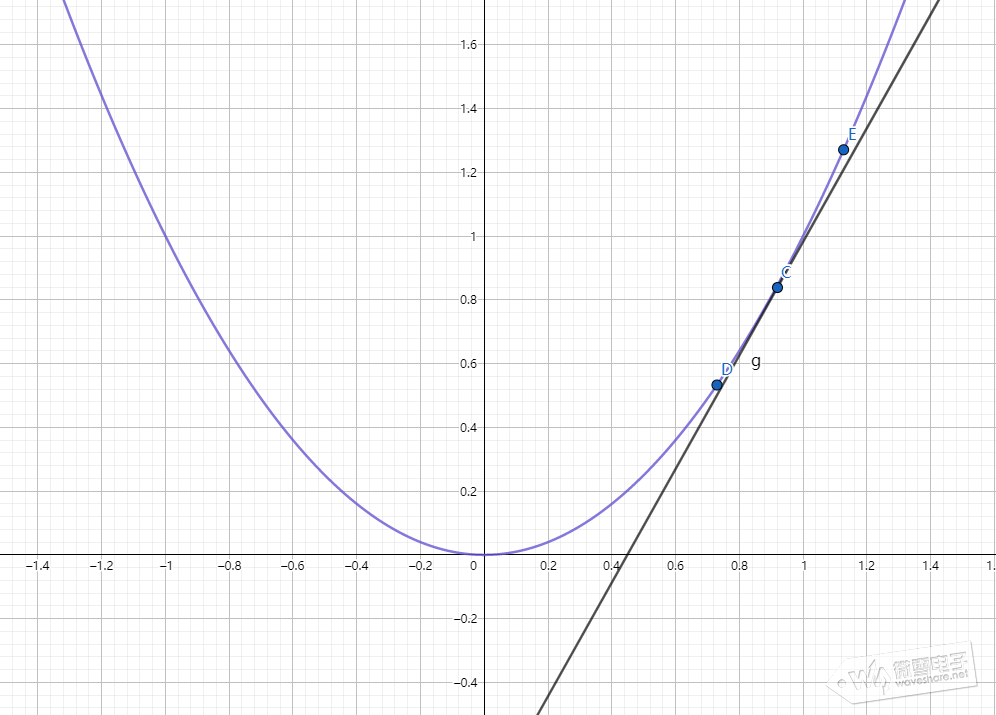
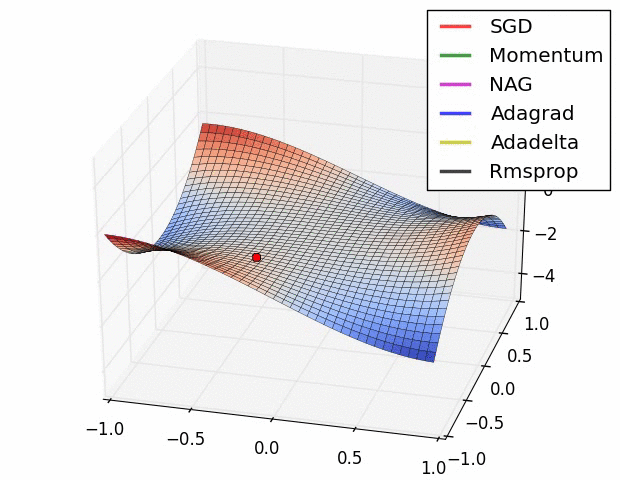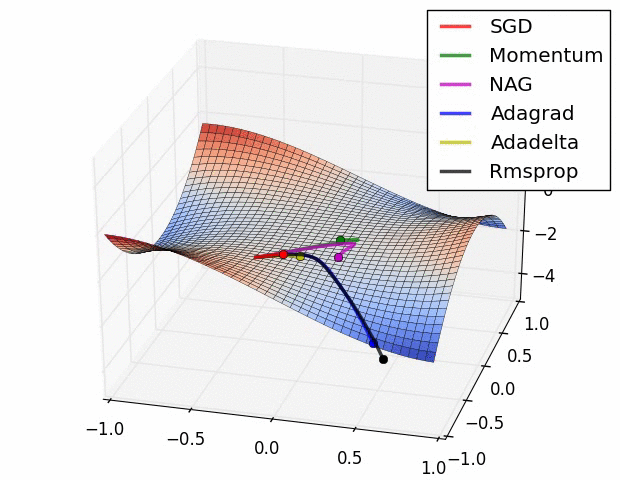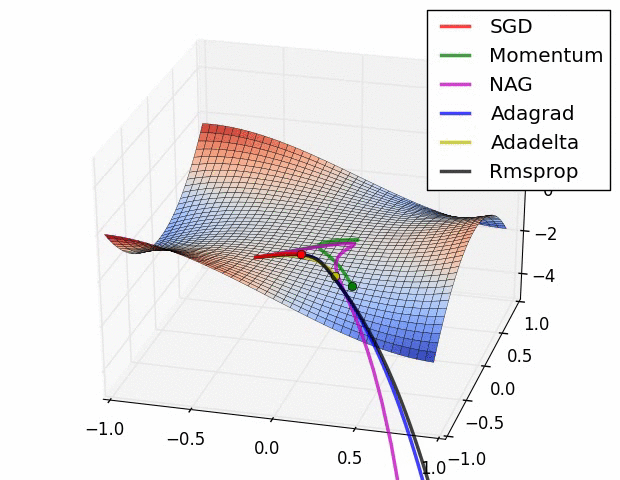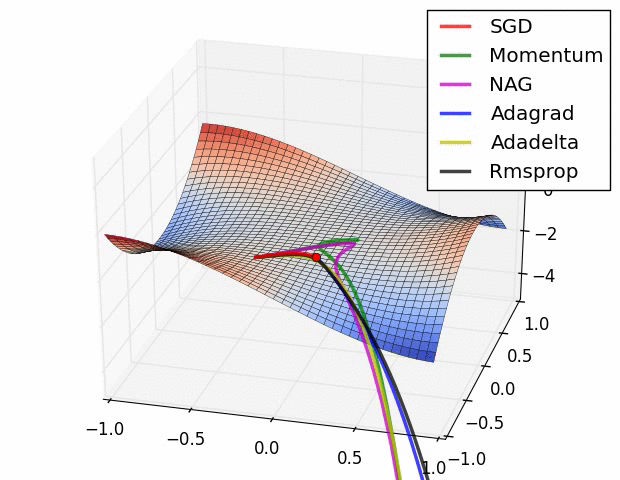
③、梯度下降法 什么是梯度下降？跟神经网络逼近或拟合任意连续函数能力之间有什么关系？ 首先回顾下神经网络工作方式，第一个阶段是，神经网络输入样本数据经过前向传递到达输出层得到预测结果；第二阶段是，使用不同计算方式(使用不同的损失函数)计算样本预测结果和样本目标结果的差异并以此作为调整权重偏置的依据，然后回传到上层网络。要想一个网络能拟合任意连续函数，就需要损失函数越小越好，所以需要约定一个方向使每训练完一批次的样本数据得到预测结果和目标结果的差异越来越小，这个使差异越来越小的方向可认为是我们要的梯度下降。梯度是高等数学中的基本概念，对于一元连续函数可理解是2维坐标轴上对函数某点的导数，对于2元函数可理解成物体在一个山峰上滚落速度最快的方向。如下图所示
上图中点C往点D的方向移动可以使函数F(x)=x^2的输出变小，定义学习率η表示C点往D点方向移动多大距离，在神经网络中学习率η表示调整权重偏置幅度，学习率η太小会使神经网络训时间增加，太大会使神经网络训练容易震荡，神经网络不容易收敛。
上图中可以看到，二元函数中，不止一个波峰波谷，不同的梯度下降法下降的快慢也不一样，神经网络要拟合逼近或拟合任意连续函数那么训练神经网络就需要进行大量运算，还需结合选取不同的梯度下降法。 更多关于梯度下降的资料请点击下面链接：
tensorflow中使用梯度下降，参数0.01表示学习率η，cross_entropy是前面定义的损失函数：
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)
三、TensorFlow构建执行神经网络 本小结构建一个二层(输入层不算)神经网络并训练MNIST手写数字集，输入层为784个神经元(将28*28二维图像转变成1维的784个像素数据)，隐藏层为1024个神经元，输出有10个神经元。
#导入需要用到的库
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
#下载MNIST手写数字集，将手写数字集28*28图像变成1维的784个数据，
mnist = input_data.read_data_sets('MNIST_data/', one_hot=True)
#定义占位符，MNIST手写数字集有60000张手写数字图片作训练样本，有10000张手写数字图片
#作测试样本
#张量x的None表示MNIST手写数字集中的图片编号，784表示降维后图片中每一个像素点
#张量y的None表示MNIST手写数字集中的图片编号，10表示0~9共10个数字概率，y为样本的目
#标结果(也称标签，导入手写数字集已经捆绑了对应的数字)
x = tf.placeholder(tf.float32, [None,784])
y = tf.placeholder(tf.float32, [None,10])
#定义权重张量w1，偏置张量b1，784个输入层神经元连接1024个隐藏层神经元
#定义隐藏层输出张量a，使用tf.nn.relu激活函数，tf.matmul(x,w1)+b1表示神经元的连接
w1 = tf.Variable(tf.truncated_normal([784,1024]), dtype = tf.float32)
b1 = tf.Variable(tf.zeros([1,1024]), dtype = tf.float32)
a = tf.nn.relu(tf.matmul(x,w1) + b1)
#定义权重张量w2，偏置张量b2，1024个隐藏层神经元连接10个输出层神经元
#定义输出层张量y_，使用tf.nn.softmax激活函数，tf.matmul(a,w2)+b2表示神经元的连接
w2 = tf.Variable(tf.ones([1024,10]))
b2 = tf.Variable(tf.zeros([1,10]))
y_= tf.nn.softmax(tf.matmul(a,w2) + b2)
#定义损失函数和梯度下降法
loss = tf.reduce_mean(-tf.reduce_sum(y*tf.log(y_), axis = 1))
train_step = tf.train.AdamOptimizer(0.0001).minimize(loss)
#初始化特殊张量
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
#每训练一个批次样本数据后后获得识别正确率
correct_prediction = tf.equal(tf.argmax(y_, axis = 1),tf.argmax(y, axis = 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
#定义好上面所有的运行方式后，使用sess.run启动tensorflow
#在1000轮训练中，mnist.train.next_batch(100)表示每轮训练取出100张样本图片，用feed_dict
#方法把100张样本图片扔进占位符x，y进行训练，train_step参数是上面定义好的网络权重和偏
#置的调整方法
#每训练100轮就检验一次MNIST手写数据集中的10000张测试图片
for i in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict = {x:batch_xs,y:batch_ys})
if i % 100 == 0:
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y: mnist.test.labels}))
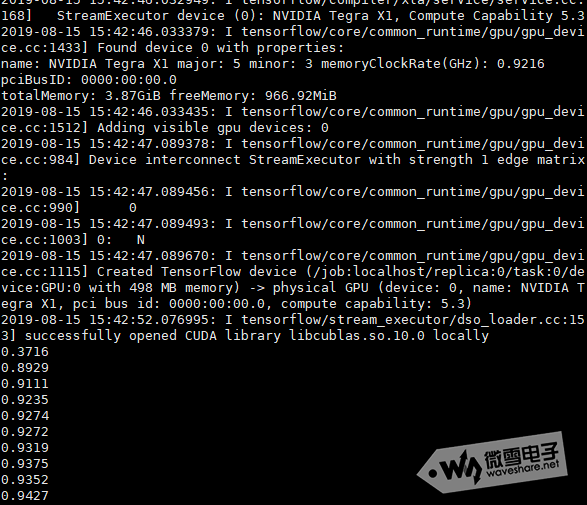
实际训练结果如下图所示
第一次训练时，输出准确率只有37.16%，最终训练的准确率为94.27%。感兴趣读者可参考上面代码在JetsonNano上进行测试。 MNIST手写数字集相关请参考下面链接：
以上资料由waveshare team整理。 Tab标签: Jetson Nano系列教程 TensorFlow python
